Reference Pages
Bioengineering

    Scroll back to top

    Conceptual framework for accounting

    Conservation—the preservation of a physical quantity during movement, transformation, or reaction—is a fundamental concept in engineering and science. Along with the second law of thermodynamics (the disorder in the universe spontaneously increases), a handful of conservation principles provide the governing laws for virtually all physical behavior. Engineers mathematically describe these laws in conjunction with initial or boundary conditions. The foundations of many fields of engineering, including bioengineering, are based on understanding and applying conservation laws.

    These laws can be applied to total mass, mass and moles of elements, linear and angular momentum, net electrical charge, and total energy. These laws have become axioms that serve as the fundamental basis for problem solving across engineering disciplines.

    Not all extensive physical properties are conserved. In other words, some extensive properties are created or destroyed during changes in or to the system. Those that are not conserved must be described using an accounting equation, a more generalized version of the conservation equation.

    An accounting equation is a mathematical description of the movement, generation, consumption, and accumulation of an extensive property within a system of interest.

    Below is a list of extensive properties that can be counted:

    • Total mass
    • Mass of individual species
    • Mass of individual element
    • Total moles
    • Moles of individual species
    • Moles of individual element
    • Total energy
    • Thermal energy
    • Mechanical energy
    • Electrical energy
    • Net electrical charge
    • Positive electrical charge
    • Negative electrical charge
    • Linear momentum
    • Angular momentum

    Attention!

    Callout Card

    Note that volume is not on this list. Compressible fluids (especially gases) may invalidate volume-based accounting equations. If volumes are given, use density to convert to mass values and then use a mass accounting equation.

    All the extensive properties listed above can be counted in accounting equations, but only a subset of these extensive properties is always conserved. Below is a complete list of extensive properties that are conserved in all situations (except nuclear reactions):

    • Total mass
    • Mass of individual element
    • Moles of individual element
    • Total energy
    • Net charge
    • Linear momentum
    • Angular momentum

    Process to use Accounting equations

    To be able to write an accounting statement, three items are necessary:

    1. The extensive property to be counted must be specified.
    2. The system and its surroundings must be defined by specifying a boundary.
    3. A time period must be specified.
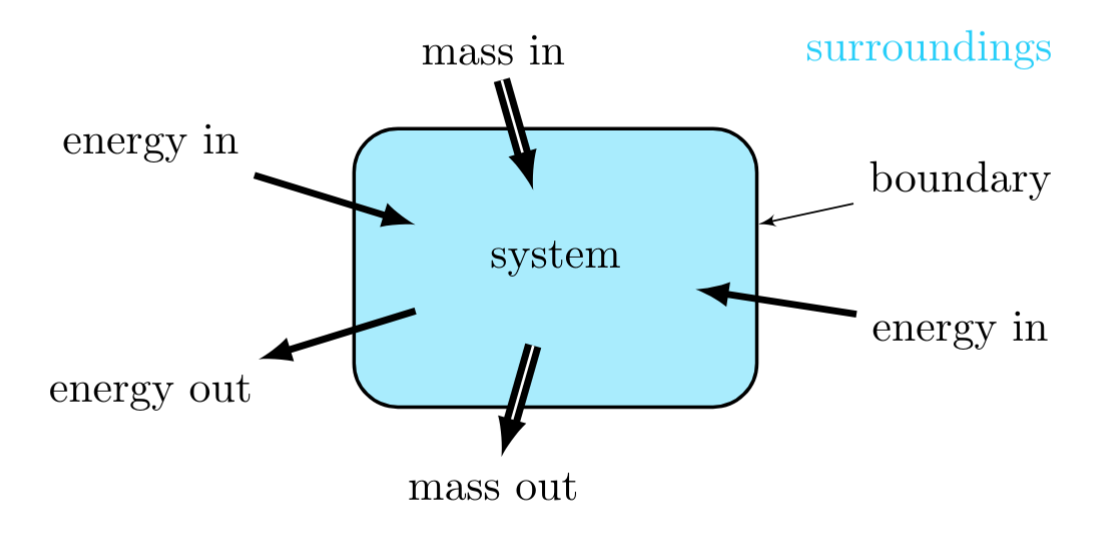
      4. System Diagram: A schematic representation of a system illustrating its key features, including system boundaries and depictions of energy and mass flows.

    Forms of Accounting Equations

    Mathematically, we illustrate both these concepts:

    Accounting (insert display equation box here)

    $$ Input - Output + Generation - Consumption = Accumulation $$

    and Conservation (insert display equation box here).

    $$ Input - Output = Accumulation $$

    or (insert display equation box here)

    $$ Accumulation=Final Condition-Initial Condition $$

    Accounting equations can be represented in three forms:

    • Algebraic
    • Differential
    • Integral

    The following equations will be shown with \( \Psi \) representing any extensive property.

    Algebraic Accounting Equations

    Algebraic accounting equations are generally applied to extensive properties within a defined system and time period. Algebraic equations can be applied when discrete quantities or “chunks” of extensive property are involved. They cannot be applied when rates or time dependent terms are involved.

    Algebraic Accounting Equation.
    $$ \Psi_{in} - \Psi_{out}+ \Psi_{gen} - \Psi_{cons} = \Psi^{sys}_{acc} $$

    Differential Accounting Equations

    Differential accounting equations are used when we have flow rates. A flow rate describes the transport of an extensive property over a period of time. We can represent the rate with a dot over the variable, \( \dot{\Psi} \).

    $$ \dot{\Psi}_{in}-\dot{\Psi}_{out}+\dot{\Psi}_{gen}-\dot{\Psi}_{cons}=\dot{\Psi}^{sys}_{acc}=\frac{d\Psi}{dt} $$

    Integral Accounting Equations

    Integral balances are most useful when trying to evaluate conditions between two discrete time points. Integral accounting equations can be written to incorporate rates of change of an extensive property. When developing an integral balance, you can write the differential balance equation and integrate it between the initial and final times.

    $$ \int_{t_f}^{t_0}{\dot{\Psi}_{in}dt}-\int_{t_f}^{t_0}{\dot{\Psi}_{out}dt}+ \int_{t_f}^{t_0}{\dot{\Psi}_{gen}dt}-\int_{t_f}^{t_0}{\dot{\Psi}_{cons}dt}= \int_{t_f}^{t_0}{\dot{\Psi}^{sys}_{acc}dt} $$

    Use the table below to ask yourself critical questions about the problem to identify what type of accounting equation is needed.

    Algebraic Differential Integral
    Can it incorporate discrete transfer of extensive property? Yes No Sometimes
    Does it involve a time interval? Finite Ongoing Finite
    Can it incorporate rates? No Yes Yes
    What is the dimension of the equation? Extensive Property Extensive Property/time Extensive Property

    Accumulation

    The Accumulation term describes the net gain or loss of an extensive property contained within a system. When an Accumulation term is present, the amount of extensive property in the system has changed during the time period of interest. There are two terms that describe the characteristics of the Accumulation term of a system: steady-state or dynamic. Steady-state is a condition in which the values of all the variables in a system (e.g., temperature, pressure, volume, and flow rate) do not change with time, although minor fluctuations about constant mean values may occur. Let us illustrate this by using a photography analogy. If you take

    multiple, imaginary “snapshots” of a steady-state system over a time period, each snapshot should look the same as the previous one. The initial and final conditions and all the intermediate snapshots of the system are identical or nearly so. The snapshots show that no quantity of the extensive property has accumulated in the system.

    A common misconception is that systems with Input and Output terms cannot be in steady-state. This is false. Systems can have Input and Output terms, as well as Generation and Consumption terms, and still operate in steady-state. What makes a system steady-state is that it does not change over time, nor is there positive or negative accumulation of the extensive property within the system of interest.

    Example Conservation Problem

    Example Problem: Consider the chemical reaction for photosynthesis. #undefined

    Given the chemical formula for photosynthesis, balance the moles of glucose and oxygen. Does this system follow the rules of conservation?

    $$ 6 CO_2 + 6 H_2O + light \rightarrow C_6H_{12}O_6 + 6O_2 $$

    The product chemical species—1 mole of glucose and 6 moles of oxygen—are counted as generated. The total amount of glucose and oxygen gas has increased in the system and the universe. On the other hand, the reactant chemical species—6 moles of carbon dioxide and 6 moles of water—have been consumed simultaneously, because the total amount of carbon dioxide and water has decreased in the system and in the universe.