Reference Pages
Bioengineering

    Scroll back to top

    Variables, Units, Dimensions

    In biological and medical engineering, the ability to quantify and track physical variables is fundamental to solving complex problems. The majority of figures used in these technical calculations denote the scale of measurable physical properties—variables that are either directly observed or derived by performing arithmetic operations on other data points. Common examples include a system's mass, its spatial length, thermal state, or rate of travel. Generally, these variables are expressed as a combination of a scalar value (the number) and a specific unit (the standard of measurement), such as 6 mL/min.

    A unit serves as a standardized, agreed-upon quantity for a specific variable, established through legal standards or scientific convention. It is essential to include these units in all engineering work to ensure the data is meaningful. For instance, stating that "adult human cardiac output is 5" provides no useful information; however, specifying "5 L/min" clearly defines the volume of blood moving through the system over time.

    A frequent oversight by novice engineers is the omission of units in their documentation. Some believe they can manage the units mentally without recording them, but this habit often results in calculation errors. For this reason, professional engineers almost never leave units out of their work. Furthermore, complex variables like energy or force are typically broken down into combinations of seven fundamental base quantities. In this context, a "dimension" refers to the qualitative nature of a physical variable rather than a specific numerical scale.

    Learn More

    Need more explanation? See more content in these references

    This content has been adapted from multiple sources including:

    Units of Interest

    Typical Units in SI and English Systems

    Typical Units in SI and English Systems: Dimensions

    DimensionSIUS
    Lengthmeter (m)foot (ft)
    Masskilogram (kg)pound mass (lb)
    Timesecond (s)second (s)

    Typical Units in SI and English Systems: State properties

    Pounds per square inch (PSI)
    State propertySIUS
    Pressure1 Pa = N/m\( ^2 \) = J/m\( ^3 \)
    Volumem\( ^3 \)ft\( ^3 \)
    Temperaturedegrees Celcius (\( ^{\circ} \)C)degrees Fahrenheit (\( ^{\circ} \)F)
    Absolute TemperatureKelvin (K)degree Rankine (\( ^{\circ} \)R)
    Internal Energy, EnthalpyJoules (J)British thermal Unit (Btu)
    Newton-meter (N\( \cdot \)m)Foot-pound force (ft\( \cdot \)lbf)
    Entropy(J/K)Btu/\( ^{\circ} \)R

    Useful Conversions

    Pressure

    Pressure unit conversions
    $$ \begin{aligned} 1~\textrm{standard atm} &= 1.01325 ~\textrm{bar} = 1.01325 \times 10^{5} ~\textrm{Pa} = 14.696~\textrm{psi} \\ &= 760~\textrm{mmHg} = 29.92~\textrm{inHg}\end{aligned} $$

    Temperature

    Temperature unit conversions
    $$ \begin{aligned}\textrm{Fahrenheit to Celcius:}&~ ^{\circ}\textrm{C} = (^{\circ}\textrm{F} -32)X (9/5) \\ \textrm{Celsius to Kelvin:}&~ ^{\circ}\textrm{K} = ^{\circ}\textrm{C} + 273.15\end{aligned} $$

    Energy

    Extensive and Intensive Properties

    Physical characteristics are categorized as either extensive or intensive based on how they react to changes in system size.

    Extensive Properties

    An extensive property is a value that represents the total sum of all non-interacting parts within a system. Consequently, the magnitude of an extensive property is directly tied to the dimensions of the system or the amount of matter present. To identify one, ask if the value would double or drop by half if the system's size were adjusted accordingly. If the value changes with the scale, it is extensive. These properties are unique because they can be "counted" or tracked in balance equations. Examples include total mass, molar amounts, specific chemical species, electrical charges, momentum, and various forms of energy.

    Intensive Properties

    Conversely, an intensive property remains constant regardless of the system's total size or the volume of the sample collected. If you were to divide or multiply the system’s scale, an intensive property would stay exactly the same. Because these values do not scale with the amount of material, they cannot be used for counting in conservation or accounting formulas. Common intensive properties include temperature, pressure, density, and the fractional concentration of components (mass or mole fractions) within a mixture. For example, if 1 kg of water is at 25°C and you add another kilogram of water at the same temperature, the resulting 2 kg of water remains at 25°C. Since the temperature does not double, it is classified as intensive.

    Scalar and Vector properties

    Physical variables are further divided into scalars and vectors. A scalar is a quantity that is fully described by its magnitude alone. A vector, however, requires both a magnitude and a specific spatial orientation. Vectors must be defined in relation to a fixed starting point or origin within a coordinate system (such as Cartesian, cylindrical, or spherical). In technical literature, vectors are often identified by an arrow symbol above the variable. Mathematically, multiplying two scalars results in another scalar. However, multiplying a scalar by a vector produces a new vector; if the scalar is positive, the direction remains the same, whereas a negative scalar reverses the direction. A classic application of this is multiplying mass (a scalar) by acceleration (a vector) to determine force (a vector).

    Extra!

    Callout Card

    Check out this great resource for unit conversions!

    Engineering ToolBox

    Vectors bases

    To describe vectors mathematically, we write them as a combination of basis vectors. An orthonormal basis is a set of two (in 2D) or three (in 3D) basis vectors which are orthogonal (have 90° angles between them) and normal (have length equal to one). We will not be using non-orthogonal or non-normal bases.

    Any other vector can be written as a linear combination of the basis vectors:

    Components of a vector. #rvv-ec
    $$ \vec{a} = a_1 \,\hat{\imath}+ a_2 \,\hat{\jmath} + a_3 \,\hat{k} $$

    The numbers \(a_1, a_2, a_3\) are called the components of \( \vec{a} \) in the \( \,\hat{\imath}, \hat{\jmath}, \hat{k} \) basis. If we are in 2D then we will only have two components for a vector.

    Length of vectors

    The length of a vector \( \vec{a} \) is written either \( \| \vec{a} \| \) or just plain \(a\). The length can be computed using Pythagorus’ theorem:

    Pythagorus' length formula. #rvv-ey
    $$ a = \|\vec{a}\| = \sqrt{a_1^2 + a_2^2 + a_3^2} $$

    First we prove Pythagorus' theorem for right-angle triangles. For side lengths \(a\) and \(b\) and hypotenuse \(c\), the fact that \(a^2 + b^2 = c^2\) can be seen graphically below, where the gray area is the same before and after the triangles are rotated in the animation:

    Pythagorus' theorem immediately gives us vector lengths in 2D. To find the length of a vector in 3D we can use Pythagorus' theorem twice, as shown below. This gives the two right-triangle calculations:

    $$ \begin{aligned} \ell^2 &= a_1^2 + a_2^2 \\ a^2 &= \ell^2 + a_3^2 = a_1^2 + a_2^2 + a_3^2. \end{aligned} $$

    Click and drag to rotate.
    Warning: Length must be computed in a single basis. #rvv-wl
    The Pythagorean length formula can only be used if all the components are written in a single orthonormal basis.

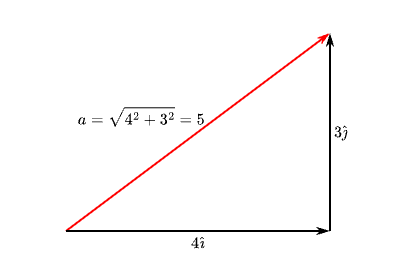
    Computing the length of a vector using Pythagorus' theorem.

    Some common integer vector lengths are \( \vec{a} = 4\hat\imath + 3\hat\jmath \) (length \(a = 5\)) and \( \vec{b} = 12\hat\imath + 5\hat\jmath \) (length \(b = 13\)).