Reference Pages
Bioengineering

    Scroll back to top

    Overview - types of Energy

    An open system allows the exchange of an extensive property through bulk material transfer with its surroundings. In an open system, energy is exchanged through movement of material and all mass possesses energy. A closed system allows for the transfer of an extensive property through means other than bulk material transfer. Heat and work are forms of energy that transit across the system boundary in the absence of any physical material.

    It is good to remember that total energy is conserved while mechanical, electrical, and thermal energy are not conserved. This is because energy is neither created nor destroyed in the universe (except for nuclear reactions) but merely changes form.

    Potential Energy

    To consider the change in potential energy of a mass between two different positions or heights, where g is the gravitational acceleration constant, h is the height relative to a reference plane, and 1 and 2 denote the two different positions in space.

    $$ \Delta E_P = E_{P,2}-E_{P,1}= \dot{m}g (h_2-h_1) $$

    Kinetic Energy

    The kinetic energy (EK) of a system is calculated using m as the mass of a body and v as the velocity. Since kinetic energy is a scalar quantity, a direction for the velocity does not need to be denoted. Kinetic energy can also move into and out of a system with a flow rate described by \( \dot{m} \). The rate of kinetic energy is calculated as

    $$ E_K = \frac{1}{2}\dot{m}v^2 $$

    Heat and Work

    Heat and work only exist when a system, and hence a system boundary, has been established. Heat and work can only be understood as the movement of energy through direct and non-direct contacts—not bulk material transfer.

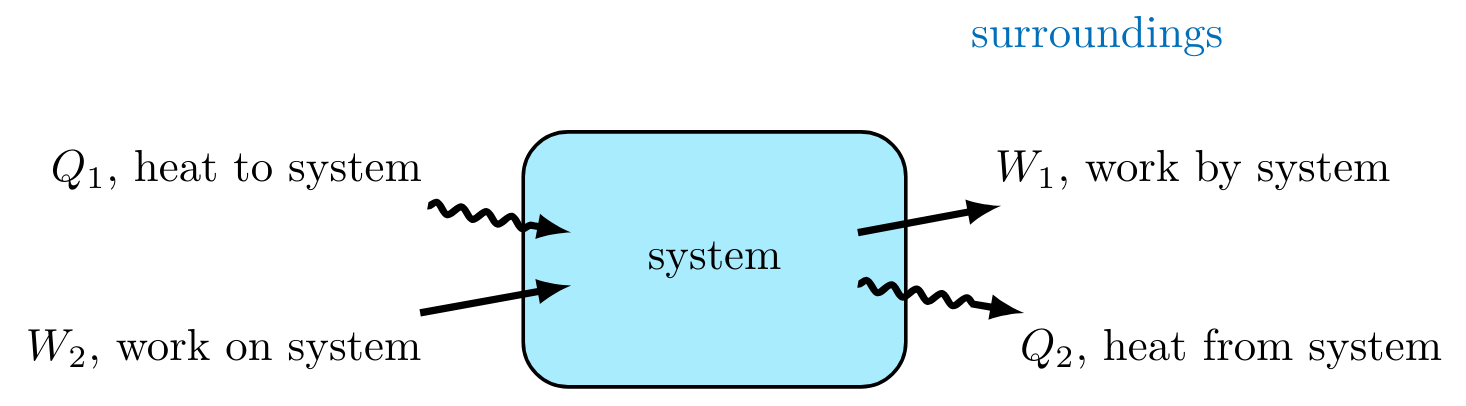
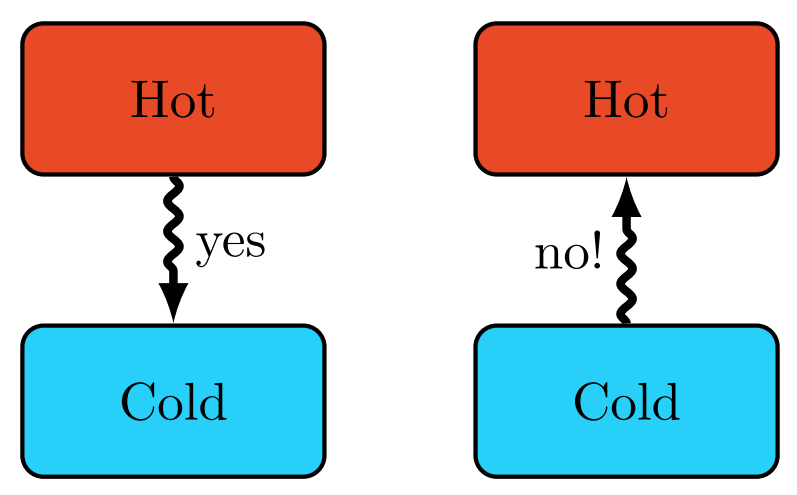
    System Diagram: A schematic representation of a system illustrating its key features, including system boundaries and depictions of energy flow.

    Heat (Q) is energy that flows due to a difference in temperature. The direction of heat flow is always from a region of higher temperature to one of lower temperature. Heat spontaneously flows from a hot object to a colder object, but not the other way around. It is impossible for any system to operate in such a way that the sole result would be an energy transfer by heat from a cooler to a hotter body.

    Heat FLow: Schematic illustration of the Clausius Statement of the Second Law.

    Heat, \( \dot{Q} \), is calculated based on the effective surface area over which the transfer occurs, A, and the temperature gradient: where h is the heat transfer coefficient (per unit area), \( T^{surr} \), is the temperature of the surroundings, and \( T^{sys} \) is the temperature of the system.

    $$ \dot{Q}=hA(T^{surr}-T^{sys}) $$

    Work (W) is energy that flows across a system boundary as a result of a driving force other than temperature. Work is a path-dependent function because it requires knowledge on how the final state of the system was reached from the initial state. Work done by a fluid flowing into the system can be calcualted using the pressure, P, area, A, and velocity, v.

    $$ \dot{W}=PAv $$

    Work can also be added to a system by mixing, stirring, etc. This nonflow work is referred to as shaft work. \( \dot{W}_{shaft} > 0 \) becasue it is added to the system.

    Conservation statements

    The total energy of a system is always conserved. The conservation equation for total energy is a mathematical description of the movement and accumulation of total energy in a system of interest. The law of the conservation of total energy states that total energy can be neither created nor destroyed, but only converted from one form into an equivalent quantity of another form of energy.

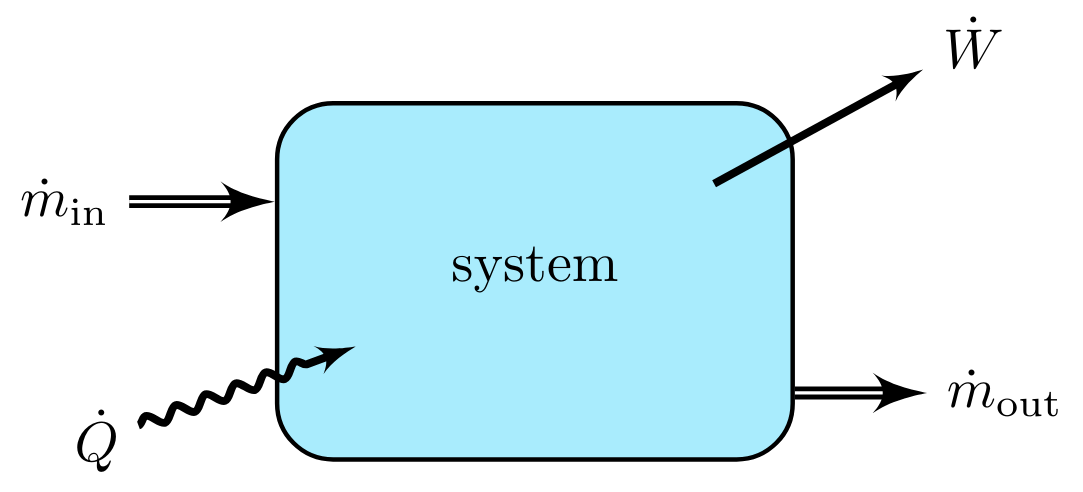
    The generic conservation equation is written to account for the movement of total energy into and out of the system by bulk mass transfer and for the transfer of heat and work across the system boundary. No Generation and Consumption terms are present, since total energy is conserved. The differential form of the conservation of total energy is:

    System Diagram: A schematic representation of a system illustrating its key features, including system boundaries and depictions of energy and mass flows.
    $$ \sum_{in} \dot{m}_{in} (\hat{E}_{P, in}+\hat{E}_{K, in}+\hat{H}_{in}) - \sum_{in} \dot{m}_{out} (\hat{E}_{P, out}+\hat{E}_{K, out}+\hat{H}_{out})+ \dot{Q} + \dot{W}_{shaft} = \frac{dE^{sys}_T}{dt} $$

    Attention!

    Note the hat on the energy terms. The hat means that they are intensive because they haven't been multiplied by mass yet. For example, \( \hat{E}_{P, in}=gh_{in} \) and \( \hat{E}_{K, in} = \frac{1}{2}v^2 \).

    Enthalpy

    Enthalpy is a state function (an intrinsic property) where only the current state matters it is the total sum of heat energy in a system. The path to convert a system from one state to another can be accomplished using the most convenient path.

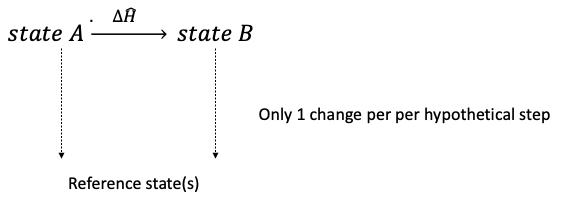
    Enthalpy state changes: Schematic illustration enthalpy changes.

    Reference state(s) are arbitrarily chosen phase, temperature, and pressure which we know a specific enthalpy of. Specific enthalpy does not depend on path, so a series of hypothetical steps from one condition to the next that are convenient for calculation can be chosen.

    Systems with chemical reactions

    During chemical reactions, rearranging the bonds between the atoms of reactants and products causes changes in the internal energy of a system. In reactions, energy is required to break the existing bonds of the reactants, and energy is released during bond formation to create the products. The difference between the final and initial energy states of the products and reactants is known as the heat of reaction.

    The heat of reaction or enthalpy of reaction \( \Delta \hat{H}_r \) is the enthalpy change for a single process reacting at a specific constant temperature and pressure in which stoichiometric quantities of reactants react completely to form products. The standard heat of reaction \( \Delta \hat{H}^{\circ}_r \) is designated with a degree symbol and is the heat of reaction when both the reactants and products are at a specified reference temperature and pressure, usually 25°C and 1 atm. The heat of reaction is always given on a per-mole basis.

    $$ \Delta \hat{H}_r = \sum_{product} (n_{product}\hat{H}_{product})-\sum_{reactant} (n_{reactant}\hat{H}_{reactant}) $$

    For Example

    For a reaction of the format, \( aA + bB \rightarrow pP + qQ \), the heat of reaction would be \( \Delta \hat{H}_r = (p\hat{H}_P)+(q\hat{H}_Q)-(a\hat{H}_A)-(b\hat{H}_B) \).

    Systems with combustion reactions

    Heat of Combustion refers to the enthalpy change required to combust 1 mol of an organic substance with oxygen. These are common in many biochemical reactions in the body.

    The heat of combustion, \( \Delta \hat{H}_c \), is the enthalpy change for a combustion process. Similar to heat of reaction, the standard heat of combustion \( \Delta \hat{H}^{\circ}_c \) is designated with a degree symbol and is the heat of reaction when both the reactants and products are at a specified reference temperature and pressure, 25°C and 1 atm. The heat of combustion is always given on a per-mole basis.

    $$ \Delta \hat{H}_c = \sum_{reactants} (\sigma_{reactants}\hat{H}_{c,reactants})-\sum_{products} (\sigma_{products}\hat{H}_{c,products}) $$

    Careful!

    Note that combustion is reactants minus products! This is important because the heat of combustion values are based on the consumption of the organic compounds, not production

    Dynamic systems

    In the case of dynamic systems, the right hand side of the equation will not be zero; instead, it will 'accumulate' internal energy. These cases occur when the system is experiencing energy changes due to mass or temperature changes of the system.

    In these cases, the right side of the equation will be converted from change in total energy to internal energy as follows

    $$ \frac{dE^{sys}_T}{dt} = m^{sys} C_v\frac{dT}{dt} $$

    giving an overall equation of

    $$ \sum_{in} \dot{m}_{in} (\hat{E}_{P, in}+\hat{E}_{K, in}+\hat{H}_{in}) - \sum_{in} \dot{m}_{out} (\hat{E}_{P, out}+\hat{E}_{K, out}+\hat{H}_{out})+ \dot{Q} + \dot{W}_{shaft} = m^{sys} C_v\frac{dT}{dt} $$