Conduction

Current page:

Steady State
Unsteady State

Conduction

Conductive (or diffusive) heat transfer is the transport of thermal energy through a medium due to temperature gradients within the material. Energy is transferred "down" the temperature gradient from high to low based on the Second Law of Thermodynamics. The net transfer of energy is due to random molecular motion.

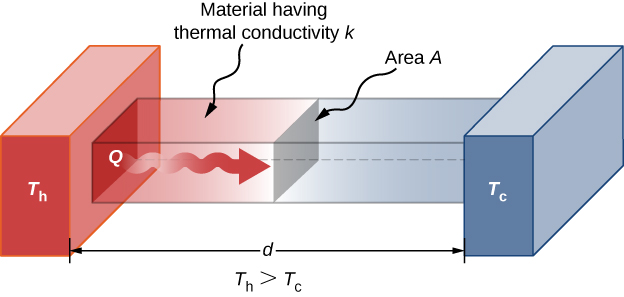
Figure 1: A temperature gradient drives heat conduction through a material. The material has constant thermal conductivity $ k $ and cross-sectional area $ A $ through which the heat flows from hot to cold along a thickness $ d $ (image source).

Fourier’s Law is used to describe conductive heat transfer:

$$ q^{''}_x = \frac{q_x}{A} = -k \frac{dT}{dx} $$

where

$ q^{''}_x [\frac{W}{m^2}] $ = flux (rate of heat flow per unit area)
$ q_x [W] $ = rate of heat flow in the x-direction
$ A [m^2] $ = surface area perpendicular to the direction of heat flow
$ T [K] $ = temperature of the medium at x
$ k [\frac{W}{mK}] $ = thermal conductivity of the medium

Thermal conductivity k describes how well a material can conduct heat.

Remember!

Always keep track of your units. To convert between Fahrenheit, Celsius, and Kelvin:

$$ ^{\circ}\textrm{C} = (^{\circ}\textrm{F} -32)*(9/5) $$

$$ K = ^{\circ}\textrm{C} + 273.15 $$

Steady State

In steady state heat conduction, temperature does not change with time. However, temperature can change with position, and this gradient drives the transfer of heat. We can consider three examples of steady state heat conduction.

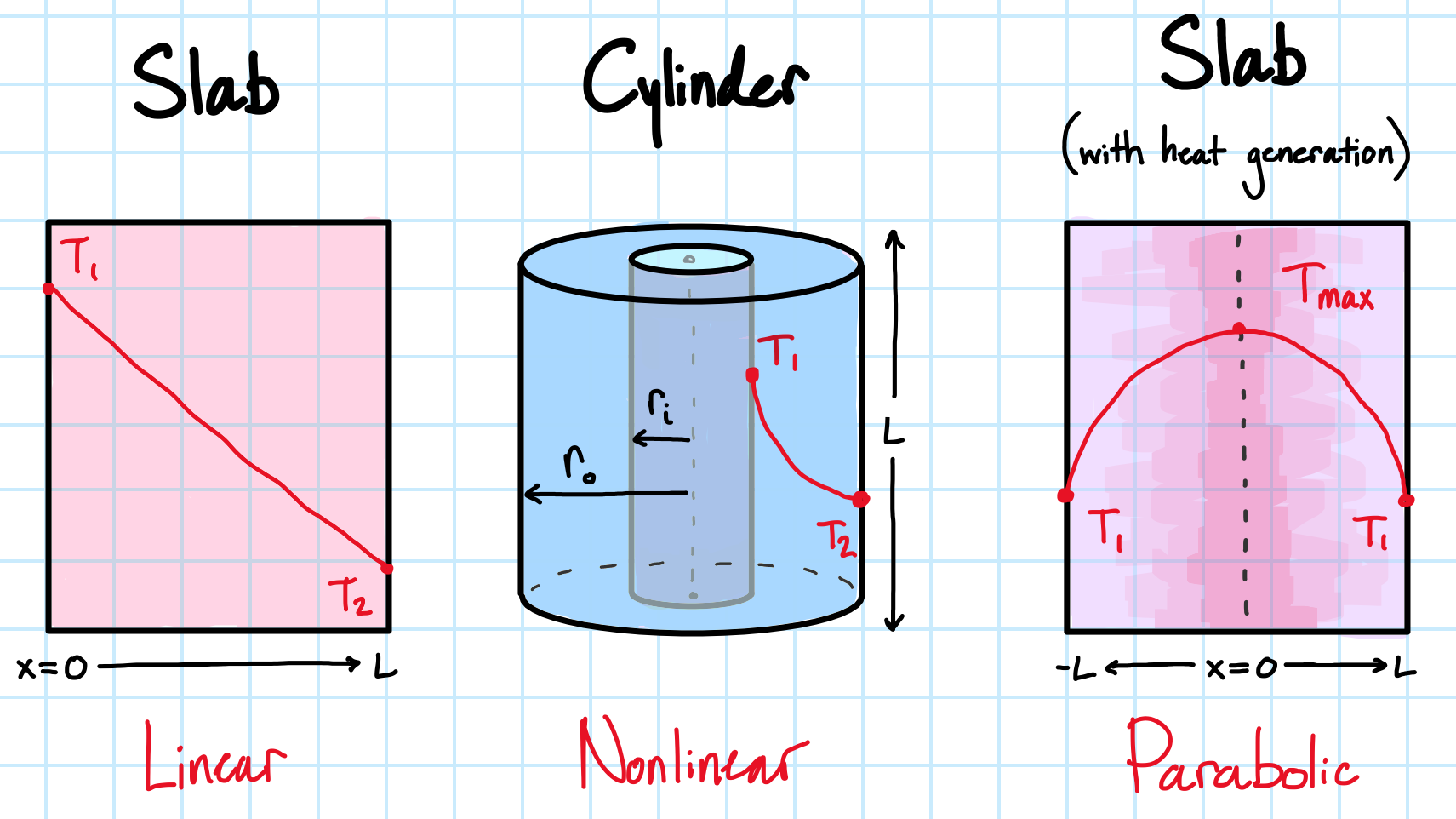
Figure 2: The temperature profile through the object varies based on its geometry and internal heat generation.

A slab has a linear temperature profile at steady-state. If the slab has a constant internal heat generation, it yields a parabolic temperature profile instead. Cylindrical and spherical geometries have nonlinear temperature profiles, as the cross-sectional area varies with position through the object.

Geometry	Temperature Profile	Heat Flow	Resistance
Slab	$ T=(T_{2}-T_{1})\frac{x}{L}+T_{2} $	$ q_{x}=\frac{T_{1}-T_{2} }{\frac{L}{kA}} $	$ \frac{L}{kA} $
Hollow Cylinder	$ T=T_{i}-\frac{T_{i}-T_{0}}{ln(r_{0}/r_{i}}ln(\frac{r}{r_{i}}) $	$ q_{r}=\frac{T_{i}-T_{0}}{\frac{ln(r_{0}/r_{i})}{2 \pi kL}} $	$ \frac{ln(r_{0}/r_{i})}{2 \pi kL} $
Hollow Sphere	$ T = T_{i}-(T_{i}-T_{0}) \frac{r-r_{i}}{r_{0}-r_{i}} \frac{r_{0}}{r} $	$ q_r = \frac{T_{i}-T_{0}}{(r_{0}-r_{i})(4 \pi r_{0} r_{i} k)} $	$ \frac{r_{0}-r_{i}}{4 \pi r_{0} r_{i} k} $

Table 1: Steady-state temperature, flow, and thermal resistance in slab (Cartesian), cylindrical, and spherical geometries.

Unsteady State

In unsteady state (or transient) heat conduction, temperature changes over time. There are three main examples of unsteady state heat conduction:

With no spatial variation
With semi-infinite geometry
With finite geometry

Geometry	Temperature Profile	Heat Flow	Resistance
Slab	\( T=(T_{2}-T_{1})\frac{x}{L}+T_{2} \)	\( q_{x}=\frac{T_{1}-T_{2} }{\frac{L}{kA}} \)	\( \frac{L}{kA} \)
Hollow Cylinder	\( T=T_{i}-\frac{T_{i}-T_{0}}{ln(r_{0}/r_{i}}ln(\frac{r}{r_{i}}) \)	\( q_{r}=\frac{T_{i}-T_{0}}{\frac{ln(r_{0}/r_{i})}{2 \pi kL}} \)	\( \frac{ln(r_{0}/r_{i})}{2 \pi kL} \)
Hollow Sphere	\( T = T_{i}-(T_{i}-T_{0}) \frac{r-r_{i}}{r_{0}-r_{i}} \frac{r_{0}}{r} \)	\( q_r = \frac{T_{i}-T_{0}}{(r_{0}-r_{i})(4 \pi r_{0} r_{i} k)} \)	\( \frac{r_{0}-r_{i}}{4 \pi r_{0} r_{i} k} \)